Recueil de formules
Terminologie, définitions
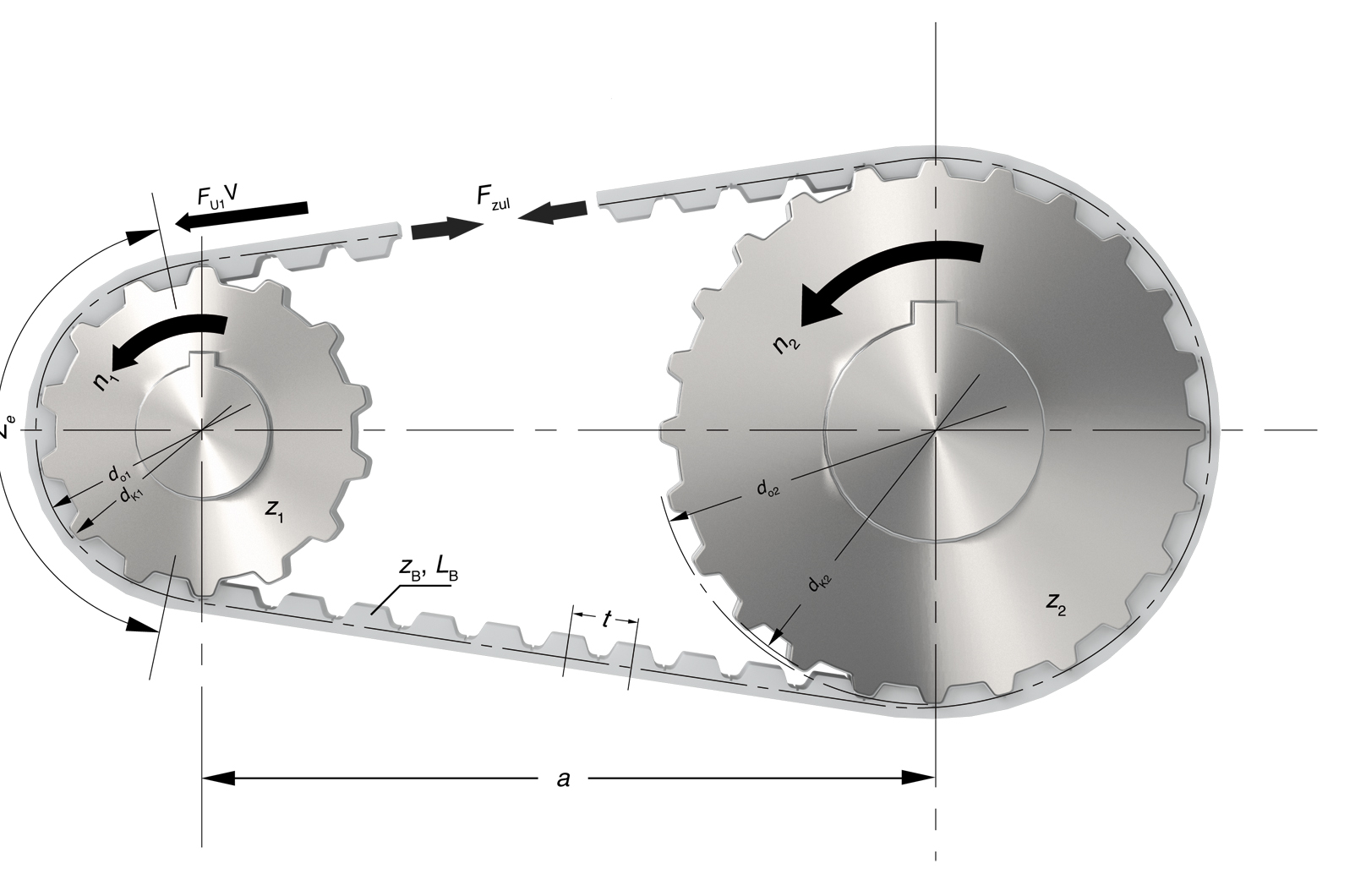
| Force périphérique | Fu | [N] | Écartement des axes | a | [mm] | |
| Résistance spécifique de la denture | FUspez | [N/cm] | Longueur de la courroie | LB | [mm] | |
| Effort en traction maximum autorisé | Fzul | [N] | Largeur de courroie | b | [mm] | |
| Mise en tension initiale | Fv | [N] | Largeur de poulie dentée | B | [mm] | |
| Force motrice arbre | Fw | [N] | Perçage poulie dentée | d | [mm] | |
| Couple de rotation | M | [Nm] | Diamètre cercle primitif | d0 | [mm] | |
| Moment d'accélération | MB | [Nm] | Diamètre de tête | dK | [mm] | |
| Couple spécifique | Mspez | [Ncm/cm] | Longueur de brin | LT | [mm] | |
| Puissance | P | [kW] | Pas | t | [mm] | |
| Puissance spécifique | Pspez | [W/cm] | Nombre de dents de courroie | zB | ||
| Moment d'inertie | J | [kgm²] | Nombre de dentures avec i=1 | z | ||
| Masse | m | [kg] | Nombre de dentures en prise | ze | ||
| Densité | ρ | [kg/dm³] | Nombre de dentures petite poulie | z1 | ||
| Vitesse | v | [m/s] | Nombre de dentures grande poulie | z2 | ||
| Vitesse de rotation | n | [min-1] | Rapport de transmission | i | ||
| Vitesse angulaire | ω | [s-1] | Temps d'accélération | tB | [s] | |
| Fréquence | fe | [s-1] |
Force périphérique
Couple de rotation
Puissance
Longueur de courroie pour i=1
Diamètre cercle primitif
Vitesse angulaire
Vitesse de rotation
Vitesse périphérique
Couple d'accélération
Moment d'inertie
Toutes les équations doivent être appliquées avec les dimensions indiquées ici.