Recueil de formules
| Force périphérique | Fu | [N] | Force de levage | FH | [N] | |
| Couple de rotation | M | [Nm] | Longueur de la courroie | LB | [mm] | |
| Puissance | P | [W] | Longueur de brin | L1, L2 | [mm] | |
| Masse à déplacer | m | [kg] | Nombre de dents de courroie | zB | ||
| Masse glissière linéaire | mL | [kg] | Nombre de dents de roue | z | ||
| Masse courroie dentée | mB | [kg] | Nombre de dents en prise | ze | ||
| Masse roue dentée | mZ | [kg] | Diamètre cercle primitif | d0 | [mm] | |
| Masse galet tendeur | mS | [kg] | Diamètre de tête | dK | [mm] | |
| Masse réduite | mred | [kg] | Diamètre galet tendeur | ds | [mm] | |
| Poids spécifique | ρ | [kg/dm3] | Perçage | d | [mm] | |
| Accélération | a | [m/s2] | Largeur de courroie | b | [mm] | |
| Accélération de la pesanteur | g | [m/s2] | Course de pré-tension | Δl | [mm] | |
| Vitesse | v | [m/s] | Élasticité spécifique | cspez | [N] | |
| Vitesse de rotation | n | [min-1] | Élasticité | c | [N/mm] | |
| Vitesse angulaire | ω | [s-1] | ||||
| Écartement des axes | sA | Écart de position | Δs | [mm] | ||
| Section linéaire utilisable | sL | Dispersion de positionnement | Ps | [mm] | ||
| Trajet de déplacement linéaire | sges | |||||
| Résistance spécifique de la denture | Ftspez | [N] | Section d’accélération | sB | [mm] | |
| Effort en traction maximum autorisé | FTzul | [N] | Section de freinage | s'B | [mm] | |
| Mise en tension initiale | FTV | [N] | Fréquence propre | fe | [s-1] | |
| Effort max. sur la ligne de courroie | FTmax | [N] | Fréquence d’excitation | f0 | [s-1] | |
| Charge sur axe | FA | [N] | Temps de déplacement pour v = constante | tv | [s] | |
| Force motrice arbre | Fw | [N] | Durée totale | tges | [s] | |
| Force de frottement | FR | [N] | Parcours total | sges | [mm] |
Toutes les équations doivent être appliquées avec les dimensions indiquées ici.
Calcul
\[F_U={2 \cdot 10^3\cdot M \over d_0}\]
Force périphérique
\[M={d_0 \cdot F_U \over 2 \cdot 10^3}\]
Couple de rotation
\[P={M \cdot n \over 9,55 \cdot 10^3}\]
Puissance
Grandeurs de calcul
force périphérique FU [N]
couple M [Nm]
puissance P [kW]
diamètre d0 [mm]

\[\omega={\pi \cdot n \over 30}\]
Vitesse angulaire
\[n={19,1 \cdot 10^3 \cdot v \over d_0}\]
Vitesse de rotation
\[v={d_0 \cdot n \over 19,1 \cdot 10^3}={\sqrt {2 \cdot s_B \cdot a \over 1000}}\]
Vitesse / vitesse périphérique
\[t_B={v \over a}={\sqrt {2 \cdot s_B \over a \cdot1000}}\]
Temps d'accélération (temps de freinage)
\[s_B={a \cdot t_B^2 \cdot 10^3 \over 2}={v^2 \cdot 10^3 \over 2 \cdot a}\]
Distance d'accélération (distance de freinage)
\[t_v={s_v \over v \cdot 10^3}\]
Durée de déplacement pour v = constante
\[s_v={v \cdot t_v \cdot 10^3}\]
Distance de déplacement pour v = constante
\[t_{ges}={t_B + t_v +t_B}\]
Durée totale
\[s_{ges}={s_B + s_v +s_B}\]
Parcours total
FU = Force d'accélération (1.) + Force de levage (2.) + Force de friction (3.)
= m * a + m * g + m * µ
force périphérique requise sur la poulie d'entraînement FU [N]
- La force d'accélération FB doit être appliquée lorsque l'entraînement linéaire doit accélérer la masse m par exemple de l'arrêt jusqu'à une vitesse finale v.
- La force de levage FH doit être appliquée si la direction de déplacement est opposée à l'accélération de la pesanteur. Dans le cas d'un mouvement linéaire horizontal, FH = 0.
- Une force doit être appliquée si une force s'applique en sens contraire au sens du mouvement, par exemple une force de frottement. Si les résistances dues aux effets de friction sont négligeables, alors FR = 0.
Calcul
mL [kg] masse du chariot linéaire à déplacer
mB [kg] masse de la courroie dentée (se reporter aux caractéristiques techniques pour le poids)
mZred [kg] masse réduite de la ou des poulies dentées
mSred [kg] masse réduite du ou des galets tendeurs
Grandeurs de calcul
masse à déplacer m [kg]
m = mL + mB + mZred + mSre
La masse d'une poulie à rebord ou d'un galet tendeur se calcule comme suit :
\[m_Z={(d_K^2-d^2) \cdot \pi \cdot B \cdot \rho \over 4 \cdot 10^6}\]
\[m_S={(d_S^2-d^2) \cdot \pi \cdot B \cdot \rho \over 4 \cdot 10^6}\]
masse de la poulie dentée mZ [kg]
masse du galet tendeur mS [kg]
La masse réduite mred d'une roue dentée ou d'un galet tendeur est une masse de substitution présentant la même inertie par rapport à la courroie dentée que la masse en rotation sur son axe.
\[m_{Zred}={m_Z \over 2 }{[1+{d^2 \over d_K^2}]}\]
\[m_{Sred}={m_S \over 2 }{[1+{d^2 \over d_S^2}]}\]
red. masse réduite de la poulie dentée mZred [kg]
red. masse du galet tendeur mSred [kg]
Un entraînement linéaire est correctement pré-tendu si, sous application de la force périphérique maximale FUmax (résultant d'une accélération ou d'un freinage) le brin à vide de la courroie reste tendu. Prévoir une mise en tension initiale minima de :
FV ≥ FU
tension initiale FV [N]
Les efforts les plus élevés Fmax surviennent dans le brin de courroie tendu lorsque la tension initiale de pose FV (statique) et la force de déplacement FU (dynamisch) agissent dans le même sens.
Fmax = FV + FU
effort maximum dans la ligne de courroie Fmax [N]
L'effort de traction admissible FTzul doit toujours présenter une marge de sécurité par rapport à l'état de tension maximum Fmax dans le brin de courroie.
(FTzul voir sous "Caractéristiques techniques").
FTzul ≥ Fmax
effort admissible sur la ligne de courroie FTzul [N]
La force statique FAsta agit à l'arrêt ou en marche à vide.
FAdyn est une des grandeurs dépendantes de la force périphérique.
FAstat = 2 * FV
effort exercé par l'axe [N]
Calcul
\begin{align}
\Delta l&={F_V \cdot L_B \over 2 \cdot c_{spez}}&& \text{Glissière linéaire}\\
\Delta l&={F_V \cdot L_B \over c_{spez}}&& \text{Chariot linéaire}\\
\Delta l&={F_V \cdot L_B \over c_{spez}}&& \text{Table linéaire}
\end{align}
Grandeurs de calcul
Course mise en tension initiale Δl [mm]
Le poste tendeur peut être placé à un endroit quelconque de la courroie.
Se reporter aux caractéristiques techniques pour les valeurs de cspez.
\[c={{L_B \over L_1 \cdot L_2}\cdot c_{spez}}\]
Élasticité c [N/mm]
\[L_B={L_1 + L_2}\]
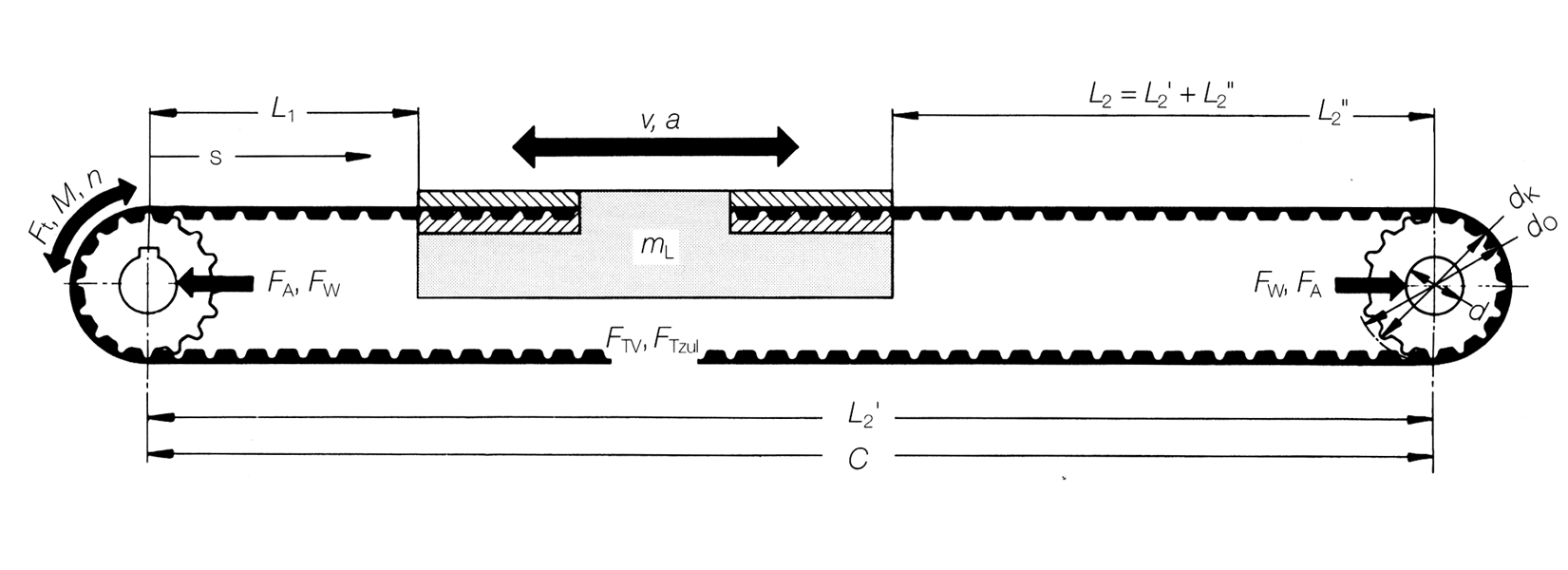
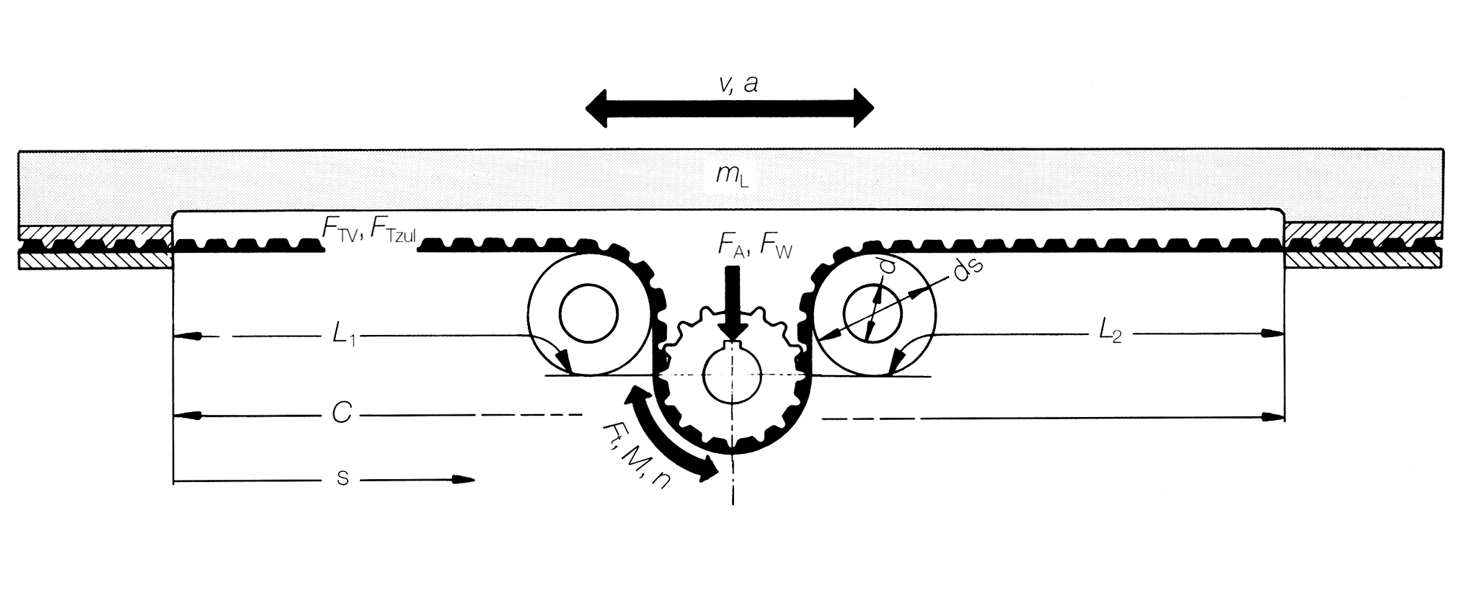
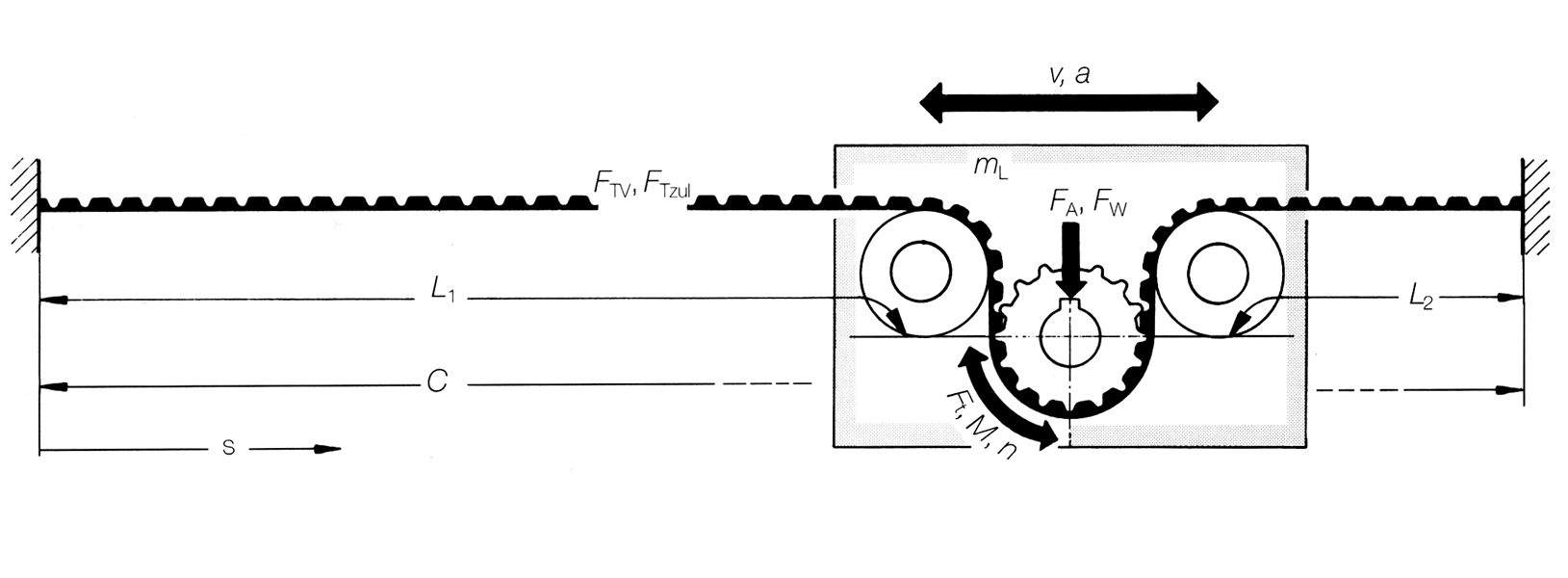
Les systèmes linéaires présentent des élasticités variables. Le comportement élastique de la glissière linéaire ou de la table linéaire dépend du rapport de longueur L1 et L2.
Ce qui implique que : Chaque position de la table linéaire présente une élasticité propre.
Cette élasticité présente un minimum cmin lorsque L1 et L2 sont de même longueur. La relation ci-après s'applique alors :
\[c_{min}={4 \cdot c_{spez} \over L_B}\]
pour L1=L2
Lorsqu'une force extérieure s'applique à une glissière linéaire, l'écart de position s peut être calculé par la formule suivante :
\[\Delta s={F \over c}\]
Écart en position Δs [mm]
Une masse liée à une courroie (système masse-ressort) subit une oscillation amortie lorsqu'elle est soumise à une impulsion.
\[f_e={{1 \over 2\pi}\sqrt{c \cdot 1000 \over m_L}}\]
Fréquence propre fe [s-1]
Il faut éventuellement vérifier pour les entraînements linéaires si des fréquences d'excitation f0 proches de la fréquence propre fe peuvent survenir.
Lors de la conception il convient d'éviter la correspondance fe = f0< (Resonanz) (résonance).
Nota : En général, la fréquence propre fe d'un entraînement linéaire est sensiblement plus élevée que la fréquence d'excitation f0 de l'entraînement, ce qui réduit le risque de résonance. Un contrôle particulier est cependant recommandé lors de l'utilisation de moteurs pas-à-pas. Mesures à prendre en cas de résonance : La raideur d'une courroie augmente avec la largeur de celle-ci.
Méthode à suivre
Les formules ci-dessus permettent de déterminer complètement les entraînements linéaires BRECO. Le type de contrôles à réaliser dépend de la tâche à remplir. Le cas échéant consulter le service technique de notre distributeur.
Cinématique, généralités
squ'il s'agit d'optimiser les temps de parcours pour un entraînement linéaire, nous recommandons de considérer les grandeurs de mouvement linéaire des formules (3).
Première approche à partir de la masse et de l'accélération
En général la masse du chariot linéaire mL et l'accélération a constituent les facteurs décisifs pour la définition d'un entraînement linéaire. Sur la page Détermination du type et de la largeur de courroie on peut déterminer la masse et l'accélération à partir du diagramme type de courroie et largeur de courroie.
Dans une première approche de la définition du matériel, il est pertinent de considérer (momentanément) les dimensions des poulies dentées. Veuillez respecter le nombre de dents et le diamètre minimal autorisés.
La station d'entraînement
L'équation (4) donne la force périphérique requise FU dans la station d'entraînement. Le couple d'entraînement M de la station d'entraînement peut être calculé à l'aide de l'équation (2), en prenant provisoirement en compte les dimensions de la roue dentée. Selon le type et le choix du moteur d'entraînement, le couple calculé M correspond plus ou moins au couple du moteur. Le choix du moteur dépend également des impératifs de positionnement. Après avoir choisi le moteur d'entrainement, le couple effectif du moteur doit être pris en compte pour calculer précisément la courroie dentée.