List of formulae, terms, definitions

Circumferencial force	F_u	[N]	Lifting force	F_H	[N]
Torque	M	[Nm]	Belt length	L_B	[mm]
Power	P	[W]	Span length	L₁, L₂	[mm]
Mass to be moved	m	[kg]	Number of belt teeth	z_B
Mass of linear slide	m_L	[kg]	Number of pulley teeth	z
Mass of timing belt	m_B	[kg]	Number of meshing teeth	z_e
Mass of pulley	m_Z	[kg]	Pitch circle diameter	d₀	[mm]
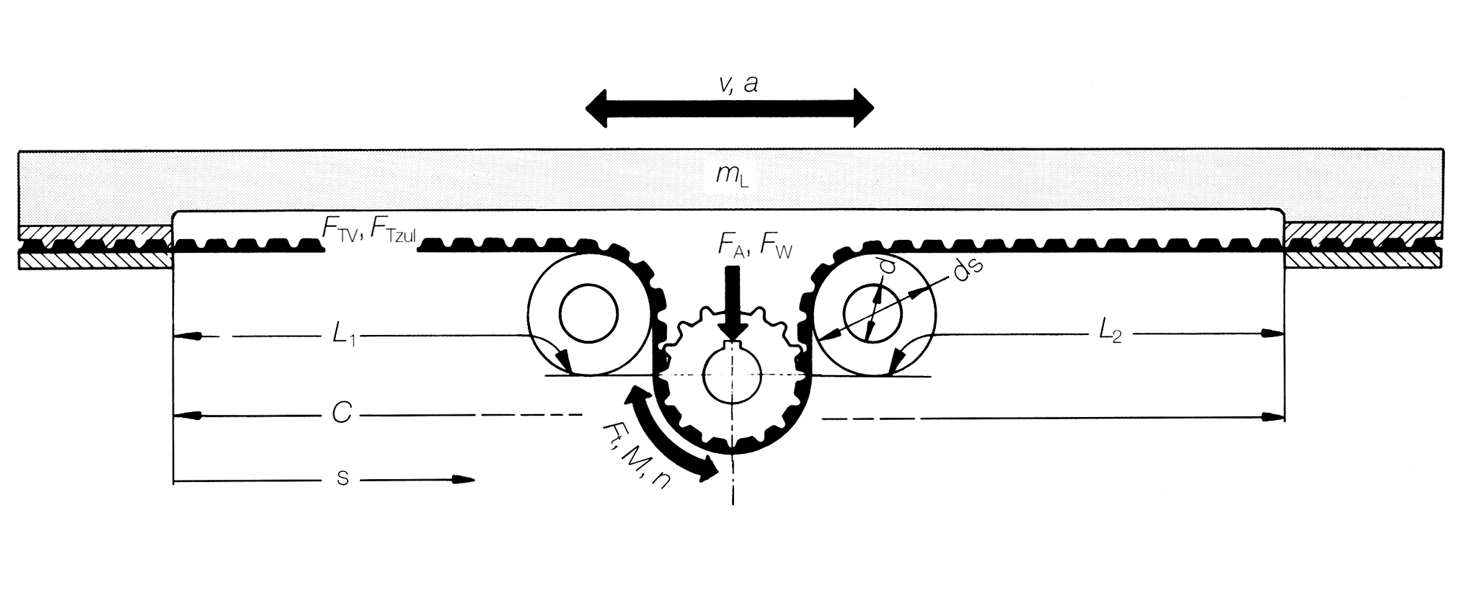
Mass of tension roller	m_S	[kg]	Crown diameter	d_K	[mm]
reduced mass	m_red	[kg]	Tension roller diameter	d_s	[mm]
specific weight	ρ	[kg/dm³]	Bore	d	[mm]
Acceleration	a	[m/s²]	Belt width	b	[mm]
Acceleration due to gravity	g	[m/s²]	Pre-tension distance	Δl	[mm]
Speed	v	[m/s]	Specific elasticity	c_spez	[N]
Rotational speed	n	[min^-1]	Elasticity	c	[N/mm]
Angular speed	ω	[s^-1]
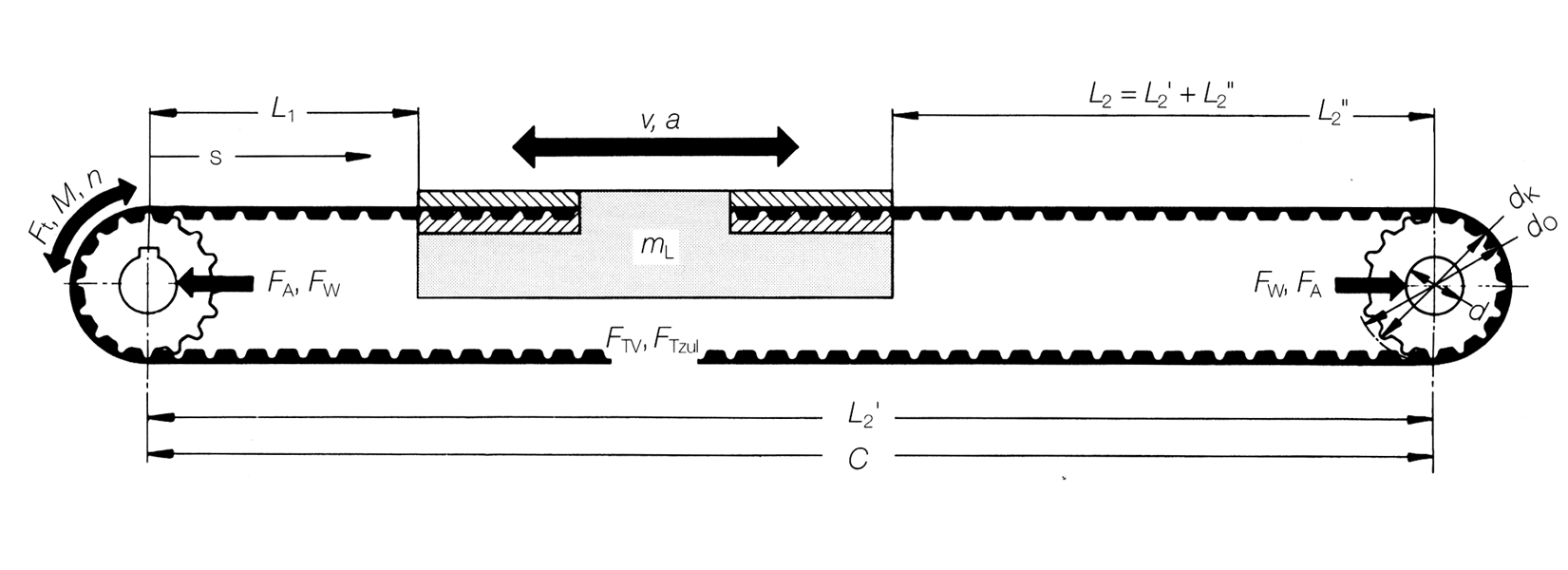
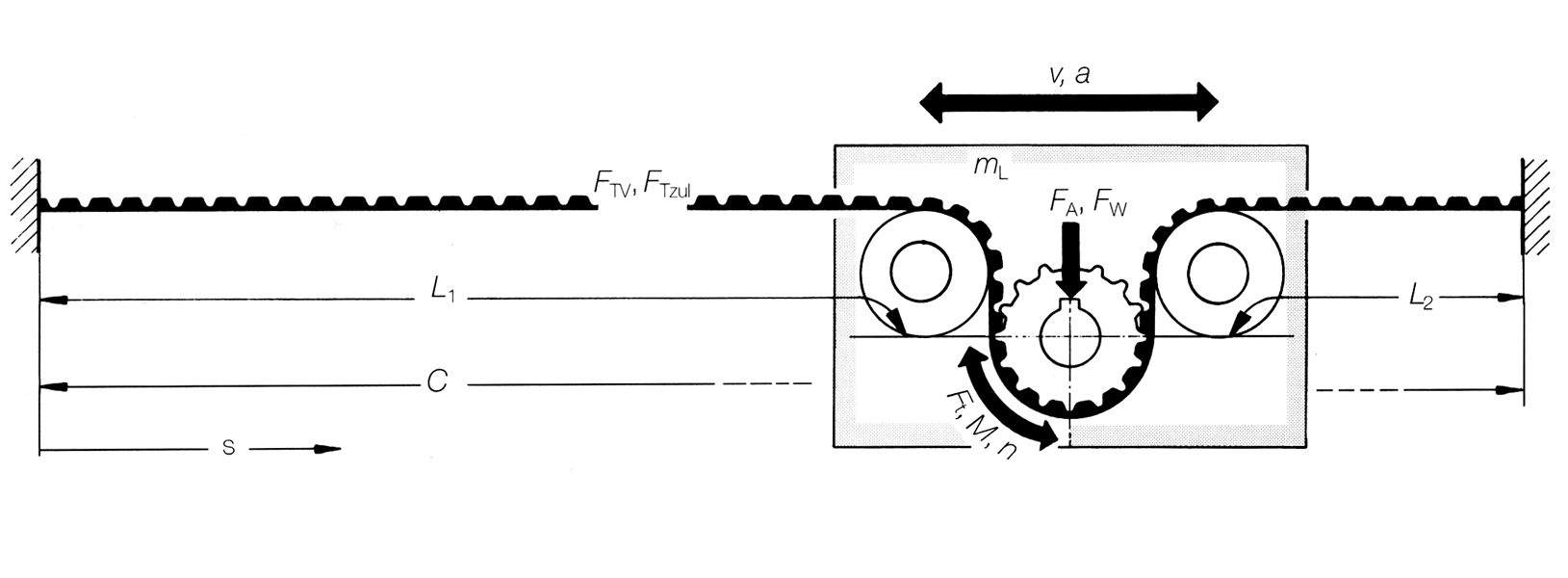
Centre distance	s_A		Positioning deviation	Δs	[mm]
Usefull linear distance	s_L		Positioning range	P_s	[mm]
total distance of travel	s_ges
Specific tooth force	F_tspez	[N]	Acceleration distance	s_B	[mm]
Admissible tensile load	F_Tzul	[N]	Braking distance	s'_B	[mm]
Pre-tension force	F_TV	[N]	Inherent frequenc	f_e	[s^-1]
max. span force	F_Tmax	[N]	Excitation frequency	f₀	[s^-1]
Centre load	F_A	[N]	Travel time with v=const.	t_v	[s]
Shaft force	F_w	[N]	Overall time	t_ges	[s]
Frictional force	F_R	[N]	Overall distance	s_ges	[mm]

Apply all equations with the dimensions mentioned here.

Calculation

$F_{U} = \frac{2 \cdot 10^{3} \cdot M}{d_{0}}$

Circumferencial force

$M = \frac{d_{0} \cdot F_{U}}{2 \cdot 10^{3}}$

Torque

$P = \frac{M \cdot n}{9, 55 \cdot 10^{3}}$

Power

Value to be calculated

circumferencial force F_U [N]
torque M [Nm]
power P [kW]
diameter d₀ [mm]

$ω = \frac{π \cdot n}{30}$

Angular speed

$n = \frac{19, 1 \cdot 10^{3} \cdot v}{d_{0}}$

Rotational speed

$v = \frac{d_{0} \cdot n}{19, 1 \cdot 10^{3}} = \sqrt{\frac{2 \cdot s_{B} \cdot a}{1000}}$

Speed / peripheral speed

$t_{B} = \frac{v}{a} = \sqrt{\frac{2 \cdot s_{B}}{a \cdot 1000}}$

Acceleration time (braking time)

$s_{B} = \frac{a \cdot t_{B}^{2} \cdot 10^{3}}{2} = \frac{v^{2} \cdot 10^{3}}{2 \cdot a}$

Acceleration distance (braking time)

$t_{v} = \frac{s_{v}}{v \cdot 10^{3}}$

Travel time when v = const.

$s_{v} = v \cdot t_{v} \cdot 10^{3}$

Travel distance when v = const.

$t_{g e s} = t_{B} + t_{v} + t_{B}$

Overall time

$s_{g e s} = s_{B} + s_{v} + s_{B}$

Total distance

FU = Acceleration force (1.) + lifting force (2.) + friction force (3.)
= m * a + m * g + m * µ

required circumferencial force at the drive pulley F_U [N]

The acceleration force F_B is necessary to accelerate the linear drive with mass m e.g. from the stand still to the limit speed v.
The lifting force F_His necessary with a movement direction opposite to the acceleration due to gravity. With horizontal linear movement is FH = 0.
A friction force is required when opposite to the moving direction a force is taking effect, e.g. friction force. Can the frictional drags be neglected is F_R = 0.

Calculation

m_L [kg] Mass of the linear slide to be moved
m_B [kg] Mass of the timing belt (belt weight, see Technical Data)
m_Zred [kg] reduced mass of pulley(s)
m_Sred [kg] reduced mass of tension roller(s)

Calculation value

mass to be moved m [kg]

m = m_L + m_B + m_Zred + m_Sre

The mass of a pulley and/or tension roller is calculated in relation to:

$m_{Z} = \frac{(d_{K}^{2} - d^{2}) \cdot π \cdot B \cdot ρ}{4 \cdot 10^{6}}$

$m_{S} = \frac{(d_{S}^{2} - d^{2}) \cdot π \cdot B \cdot ρ}{4 \cdot 10^{6}}$

Mass of the pulley m_Z [kg]
Mass of the tension roller m_S [kg]

The reduced mass m_red of a pulley and/or tension roller is an equivalent mass with equal load bearing to the effective line of the timing belt, the same as the rotational solid to the rotational axis.

$m_{Z r e d} = \frac{m_{Z}}{2} [1 + \frac{d^{2}}{d_{K}^{2}}]$

$m_{S r e d} = \frac{m_{S}}{2} [1 + \frac{d^{2}}{d_{S}^{2}}]$

red. Mass of the pulley m_Zred [kg]
red. Mass of the tension roller m_Sred [kg]

A linear drive is pre-tensioned correctly, when under maximum effective circumferencial force F_Umax (from acceleration and braking) the slack span side of the belt stayes tight. A minimum pre-tension force is to be considered:

F_V ≥ F_U

Pre-tension force F_V [N]

The highes span forces F_max are to be expected within the tight span side, when both pre-tension force F_V (static) and circumferencial force F_U (dynamisch) (dynamic) acting together.

F_max = F_V + F_U

maximum span force in the belt F_max [N]

The permitted tensile load F_Tzul has to show safety factors to the max. occurring span force F_max in the timing belt.
(F_Tzul see Technical Data).

F_Tzul ≥ F_max

permitted span force F_Tzul [N]

The static axis load F_Asta act within the stand still or under no-load conditions.
F_Adyn is a value depending on the effective circumferencial force.

F_Astat = 2 * F_V

Axis load [N]

Calculation

$\begin{aligned} Δ l & = \frac{F_{V} \cdot L_{B}}{2 \cdot c_{s p e z}} & Linear slide \\ Δ l & = \frac{F_{V} \cdot L_{B}}{c_{s p e z}} & Linear trolley \\ Δ l & = \frac{F_{V} \cdot L_{B}}{c_{s p e z}} & Linear table \end{aligned}$

Calculation value

pre-tension distance Δl [mm]

The tensioning station can be mounted at any position on the timing belt.
Values for c_spez see Technical Data.

$c = \frac{L_{B}}{L_{1} \cdot L_{2}} \cdot c_{s p e z}$

Elasticity c [N/mm]

$L_{B} = L_{1} + L_{2}$

Linear systems show a variable elasticity. The elasticity behaviour of the linear slide and/or linear bed depends on the length proportion L₁ and L₂.
That means: Each individual position of the linear bed has its own elasticity.
The elasticity shows a minimum c_min, when L₁ and L₂are equal in length. For this case the following relation is valid:

$c_{m i n} = \frac{4 \cdot c_{s p e z}}{L_{B}}$

for L₁=L₂

Is an external force acting on a linear slide a positioning deviation s results from the relation:

$Δ s = \frac{F}{c}$

Positioning deviation Δs [mm]

Under the effect of a triggered force, a mass connected to the timing belt (elasticity/mass system) assumes a damped natural vibration.

$f_{e} = \frac{1}{2 π} \sqrt{\frac{c \cdot 1000}{m_{L}}}$

Natural frequency f_e [s^-1]

If necessary, check linear drives with regard to the occurrence of excitation frequencies f₀ in the drive pulley assembly which are close to the natural frequency f_e.
For technical structures, avoid compatibility of f_e = f₀< (Resonanz) (resonance).
Note: In linear drives, the natural frequency f_e is in general considerably higher than the excitation frequency f₀ of the drive, in which case no resonance is to be expected . We recommend a special examination, if necessary, where stepping motors are used. Measures in the event of resonance: Increase the stiffness of the timing belt by choosing a larger belt width.

How to proceed

The above mentioned equations can be used to comprehensively compute BRECO linear drives. The type of the individual examinations depends on the task. If necessary, request technical support from our sales outlets.

General kinematics

If the movement sequence of the linear drive has to be timed, we recommend to proceed in accordance with the linear movement values of the equations (3).

Coarse design according to mass and acceleration

Generally, the mass of the linear slide m_L and the acceleration a represent the decisive values for the design of linear drives. The selection diagram, the belt type and timing belt width can be determined, based on mass and acceleration shown on the page Determination of belt type and belt width.In conjunction with the coarse design, we recommend to adopt the pulley dimensions (as a provisional measure). Note the permissible minimum number of teeth or minimum diameters.

Drive pulley assembly

The required circumferential force F_U in the drive pulley assembly has to be determined according to equation (4). By provisionally assuming the pulley size, it is possible to calculate the attendant drive torque M according to equation (2) for the drive pulley assembly. In how far the calculated torque M can be harmonised with the torque sequence of the motor, depends on the type and selection of the drive motor. The selection of the motor also depends on the desired servo and positioning tasks. Once the drive motor has been decided upon, the actual torque sequence of the motor has to be taken into consideration for the further precise design of the timing belt.

List of formulae, terms, definitions

Calculation

Value to be calculated

Calculation

Calculation value

Calculation

Calculation value

How to proceed

General kinematics

Coarse design according to mass and acceleration

Drive pulley assembly

MULCO-EUROPE EWIV

Quicklinks

Legal

Login

Calculation

Value to be calculated

Calculation

Calculation value

Calculation

Calculation value

How to proceed

General kinematics

Coarse design according to mass and acceleration

Drive pulley assembly