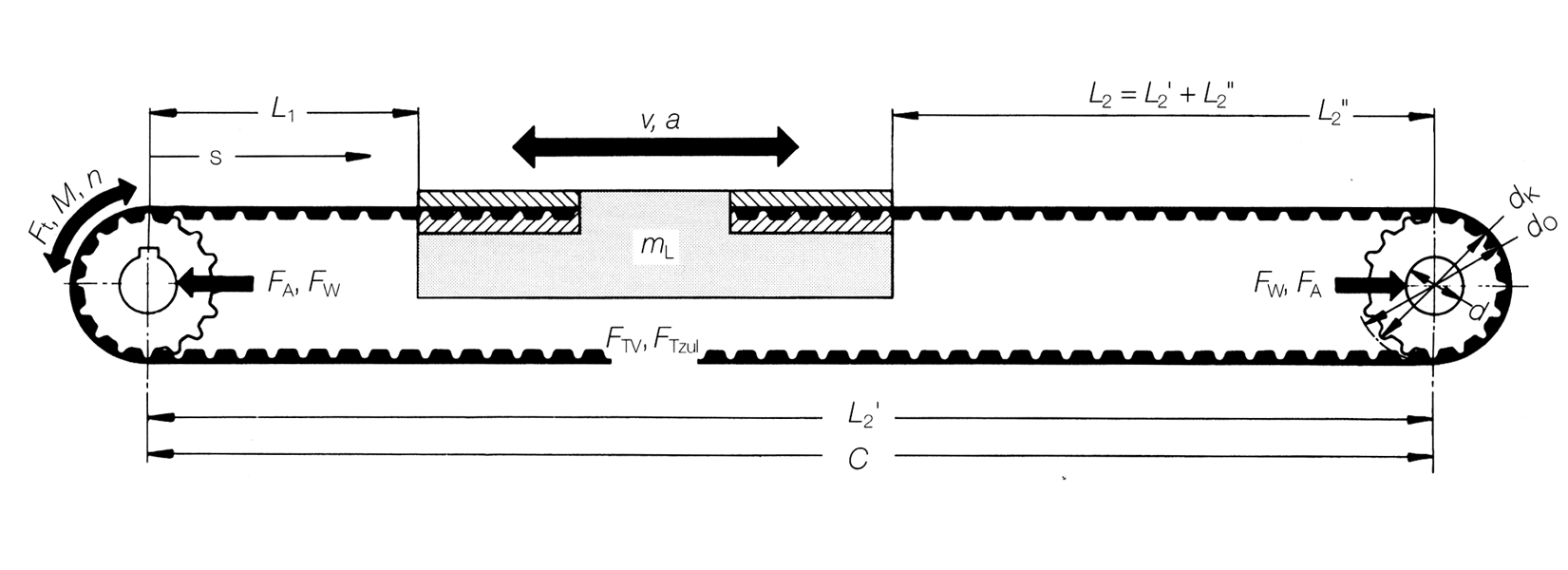
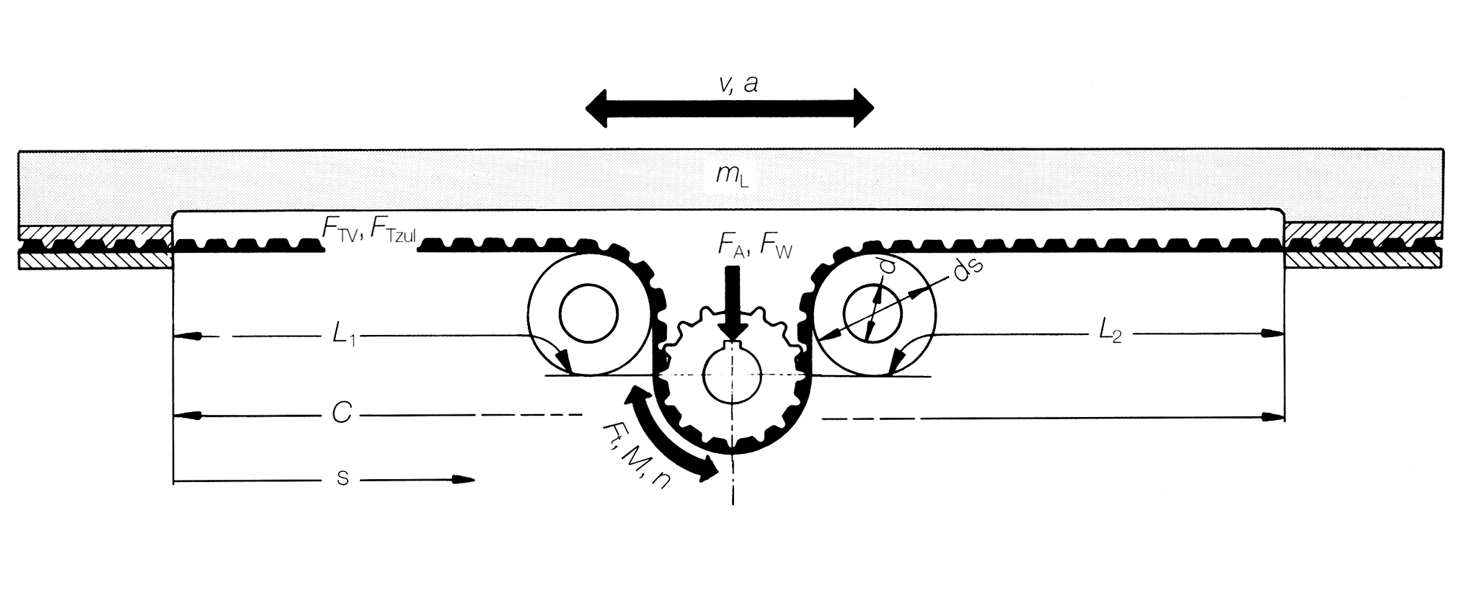
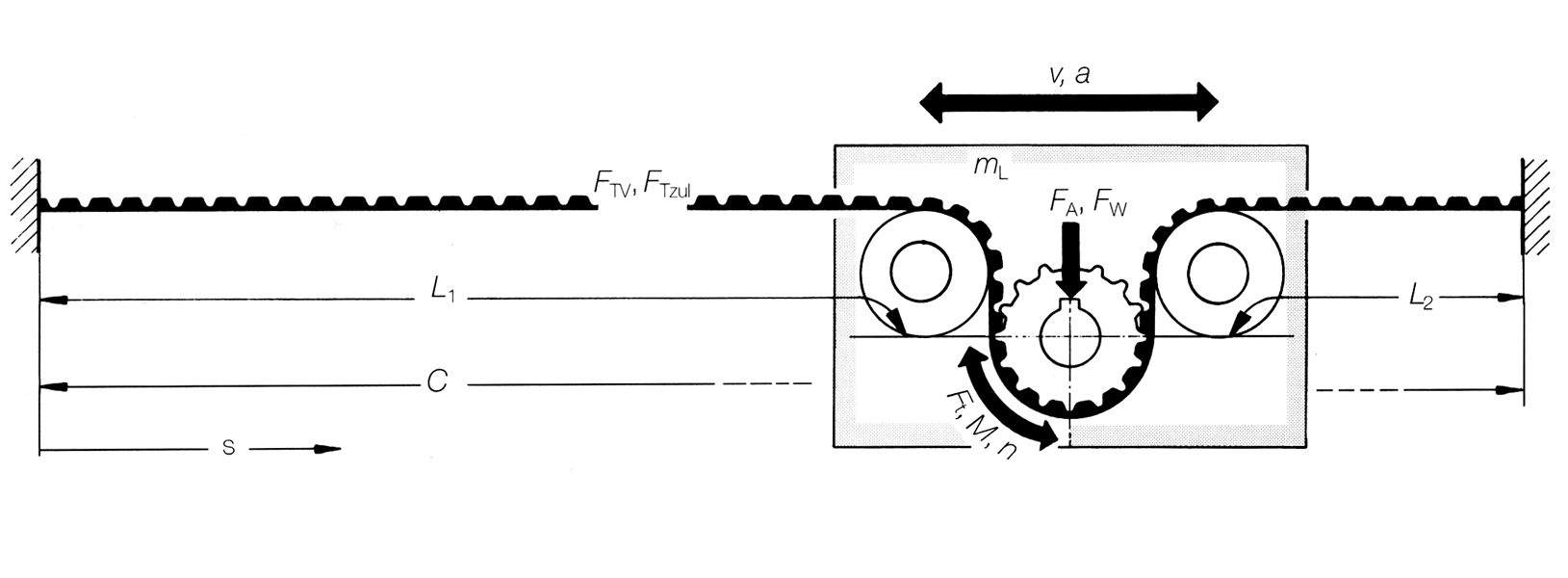
Formelsammlung

Umfangskraft	F_u	[N]	Hubkraft	F_H	[N]
Drehmoment	M	[Nm]	Riemenlänge	L_B	[mm]
Leistung	P	[W]	Trumlänge	L₁, L₂	[mm]
Zu bewegende Masse	m	[kg]	Riemenzähnezahl	z_B
Masse Linearschlitten	m_L	[kg]	Scheibenzähnezahl	z
Masse Zahnriemen	m_B	[kg]	Eingriffzähnezahl	z_e
Masse Zahnscheibe	m_Z	[kg]	Wirkkreisdurchmesser	d₀	[mm]
Masse Spannrolle	m_S	[kg]	Kopfkreisdurchmesser	d_K	[mm]
reduzierte Masse	m_red	[kg]	Durchmesser Spannrolle	d_s	[mm]
spezifisches Gewicht	ρ	[kg/dm³]	Bohrung	d	[mm]
Beschleunigung	a	[m/s²]	Riemenbreite	b	[mm]
Erdbeschleunigung	g	[m/s²]	Vorspannweg	Δl	[mm]
Geschwindigkeit	v	[m/s]	spez. Federrate	c_spez	[N]
Drehzahl	n	[min^-1]	Federrate	c	[N/mm]
Winkelgeschwindigkeit	ω	[s^-1]
Achsabstand	s_A		Positionierabweichung	Δs	[mm]
Nutzbare Linearstrecke	s_L		Positionierstreubreite	P_s	[mm]
gesamter Verfahrweg	s_ges
spezifische Zahnkraft	F_tspez	[N]	Beschleunigungsweg	s_B	[mm]
zulässige Seilzugkraft	F_Tzul	[N]	Bremsweg	s'_B	[mm]
Vorspannkraft	F_TV	[N]	Eigenfrequenz	f_e	[s^-1]
max. Trumkraft	F_Tmax	[N]	Erregerfrequenz	f₀	[s^-1]
Achslast	F_A	[N]	Fahrzeit bei v=konst.	t_v	[s]
Wellenkraft	F_w	[N]	Gesamtzeit	t_ges	[s]
Reibkraft	F_R	[N]	Gesamtstrecke	s_ges	[mm]

Alle Gleichungen sind mit den hier genannten Dimensionen anzuwenden.

Berechnung

$F_{U} = \frac{2 \cdot 10^{3} \cdot M}{d_{0}}$

Umfangskraft

$M = \frac{d_{0} \cdot F_{U}}{2 \cdot 10^{3}}$

Drehmoment

$P = \frac{M \cdot n}{9, 55 \cdot 10^{3}}$

Leistung

Berechnungsgröße

Umfangskraft F_U [N]
Drehmoment M [Nm]
Leistung P [kW]
Durchmesser d₀ [mm]

$ω = \frac{π \cdot n}{30}$

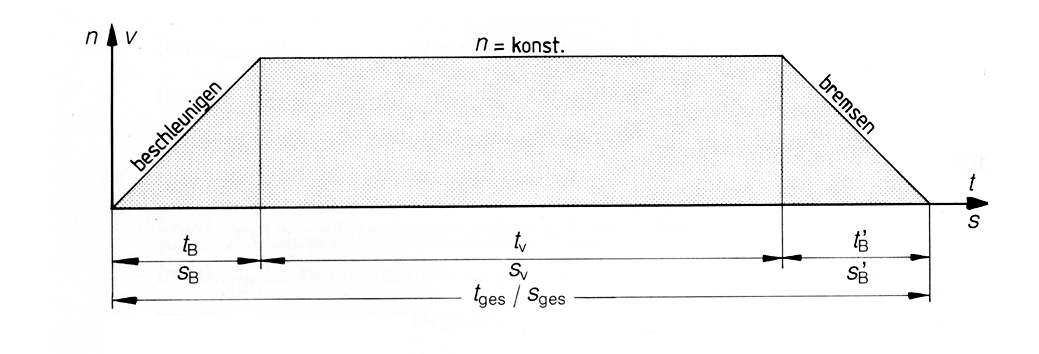
Winkelgeschwindigkeit

$n = \frac{19, 1 \cdot 10^{3} \cdot v}{d_{0}}$

Drehzahl

$v = \frac{d_{0} \cdot n}{19, 1 \cdot 10^{3}} = \sqrt{\frac{2 \cdot s_{B} \cdot a}{1000}}$

Geschwindigkeit / Umfangs-geschwindigkeit

$t_{B} = \frac{v}{a} = \sqrt{\frac{2 \cdot s_{B}}{a \cdot 1000}}$

Beschleunigungszeit (Bremszeit)

$s_{B} = \frac{a \cdot t_{B}^{2} \cdot 10^{3}}{2} = \frac{v^{2} \cdot 10^{3}}{2 \cdot a}$

Beschleunigungsweg (Bremsweg)

$t_{v} = \frac{s_{v}}{v \cdot 10^{3}}$

Verfahrzeit bei v = konst.

$s_{v} = v \cdot t_{v} \cdot 10^{3}$

Verfahrstrecke bei v = konst.

$t_{g e s} = t_{B} + t_{v} + t_{B}$

Gesamtzeit

$s_{g e s} = s_{B} + s_{v} + s_{B}$

Gesamtstrecke

FU = Beschleunigungskraft (1.) + Hubkraft (2.) + Reibkraft (3.)
= m * a + m * g + m * µ

erforderliche Umfangskraft an der Antriebsscheibe F_U [N]

Die Beschleunigungskraft F_B ist aufzubringen, wenn der Linearantrieb mit der Masse m z. B. aus der Ruhelage auf Endgeschwindigkeit v zu beschleunigen ist.
Die Hubkraft F_H ist aufzubringen, wenn die Bewegungsrichtung entgegengesetzt zur Erdbeschleunigung gerichtet ist. Bei horizontaler Linearbewegung ist F_H = 0.
Eine Reibkraft ist aufzubringen, wenn entgegengesetzt zur Bewegungsrichtung eine Kraft wirkt, z.B. Reibungskraft. Sind die Reibungswiderstände zu vernachlässigen, so ist F_R = 0.

Berechnung

m_L [kg] Masse des zu bewegenden Linearschlittens
m_B [kg] Masse des Zahnriemens (Riemengewichte siehe Technische Daten)
m_Zred [kg] reduzierte Masse der Zahnscheibe(n)
m_Sred [kg] reduzierte Masse der Spannrolle(n)

Berechnungsgröße

zu bewegende Masse m [kg]

m = m_L + m_B + m_Zred + m_Sre

Die Masse einer Zahnscheibe bzw. einer Spannrolle berechnet sich zu:

$m_{Z} = \frac{(d_{K}^{2} - d^{2}) \cdot π \cdot B \cdot ρ}{4 \cdot 10^{6}}$

$m_{S} = \frac{(d_{S}^{2} - d^{2}) \cdot π \cdot B \cdot ρ}{4 \cdot 10^{6}}$

Masse der Zahnscheibe m_Z [kg]
Masse der Spannrolle m_S [kg]

Die reduzierte Masse m_red einer Zahnscheibe bzw. einer Spannrolle ist eine Ersatzmasse mit gleicher Massenträgheit zur Wirklinie des Zahnriemens wie der Rotationskörper zur Rotationsachse.

$m_{Z r e d} = \frac{m_{Z}}{2} [1 + \frac{d^{2}}{d_{K}^{2}}]$

$m_{S r e d} = \frac{m_{S}}{2} [1 + \frac{d^{2}}{d_{S}^{2}}]$

red. Masse der Zahnscheibe m_Zred [kg]
red. Masse der Spannrolle m_Sred [kg]

Ein Linearantrieb ist richtig vorgespannt, wenn unter wirkender maximaler Umfangskraft F_Umax (aus Beschleunigung und Bremsen) der Leertrum des Riemens gestreckt bleibt. Es ist eine Mindestvorspannkraft vorzusehen von:

F_V ≥ F_U

Vorspannkraft F_V [N]

Die größten Trumkräfte F_max sind im Zugtrum zu erwarten, wenn Vorspannkraft F_V (statisch) und Verkehrskraft F_U (dynamisch) gemeinsam wirksam werden.

F_max = F_V + F_U

maximale Trumkraft im Riemen F_max [N]

Die zulässige Seilzugkraft F_Tzul muß stets Sicherheiten aufweisen gegenüber der max. auftretenden Trumkraft F_max im Zahnriemen.
(F_Tzul siehe Technische Daten).

F_Tzul ≥ F_max

zulässige Trumkraft F_Tzul [N]

Die statische Achskraft F_Asta wirkt im Stillstand oder unter Leerlaufbedingungen.
F_Adyn ist eine von der wirksamen Umfangskraft abhängige Größe.

F_Astat = 2 * F_V

Achskraft [N]

Berechnung

$\begin{aligned} Δ l & = \frac{F_{V} \cdot L_{B}}{2 \cdot c_{s p e z}} & Linear-Schlitten \\ Δ l & = \frac{F_{V} \cdot L_{B}}{c_{s p e z}} & Linear-Laufkatze \\ Δ l & = \frac{F_{V} \cdot L_{B}}{c_{s p e z}} & Linear-Tisch \end{aligned}$

Berechnungsgröße

Vorspannweg Δl [mm]

Die Spannstation kann an beliebiger Stelle des Zahnriemens angeordnet werden.
Werte für c_spez siehe Technische Daten.

$c = \frac{L_{B}}{L_{1} \cdot L_{2}} \cdot c_{s p e z}$

Federrate c [N/mm]

$L_{B} = L_{1} + L_{2}$

Linearsysteme weisen eine veränderliche Federrate auf. Das Federungsverhalten des Linearschlittens bzw. Lineartisches ist abhängig vom jeweiligen Längenverhältnis L₁ und L₂.
Das heißt: Jede Position des Lineartisches hat seine eigene Federrate.
Die Federrate weist ein Minimum c_min auf, wenn L₁ und L₂ längengleich sind. Für diesen Fall gilt die Beziehung:

$c_{m i n} = \frac{4 \cdot c_{s p e z}}{L_{B}}$

bei L₁=L₂

Wirkt eine äußere Kraft auf einen Linearschlitten, so ergibt sich die Positionierabweichung s aus der Beziehung:

$Δ s = \frac{F}{c}$

Positionierabweichung Δs [mm]

Eine am Zahnriemen verbundene Masse (Feder-Masse-System) gerät bei einem Kraftanstoß in gedämpfte Eigenschwingung.

$f_{e} = \frac{1}{2 π} \sqrt{\frac{c \cdot 1000}{m_{L}}}$

Eigenfrequenz f_e [s^-1]

Lineartriebe müssen gegebenenfalls überprüft werden, ob im Antriebssystem Erregefrequenzen f₀ auftreten, die in der Nähe der Eigenfrequenz f_e liegen.
Bei technischen Konstruktionen ist die Übereinstimmung f_e = f₀< (Resonanz) zu vermeiden.
Hinweis: In Lineartrieben liegt die Eigenfrequenz f_e im Allgemeinen deutlich höher als die Erregerfrequenz f₀ des Antriebes, Resonanz ist dann nicht zu erwarten. Eine besondere Prüfung wird gegebenenfalls beim Einsatz von Schrittmotoren empfohlen. Maßnahmen bei Resonanz: Federsteife des Zahnriemens erhöhen durch größere Riemenbreite.

Vorgehensweise

Mit den vorgenannten Gleichungen können BRECO-Linearantriebe umfassend berechnet werden. Es hängt von der Art der Aufgabenstellung ab, welche Untersuchungen im Einzelnen erforderlich sind. Gegebenenfalls ist die technische Beratung durch unsere Vertriebspartner anzufordern.

Allgemeine Kinematik

Wenn der Bewegungsablauf des Lineartriebes zeitlich zu optimieren ist, empfehlen wir, nach den linearen Bewegungsgrößen der Gleichungen (3) vorzugehen.

Grobauslegung nach Masse und Beschleunigung

In der Regel sind die Masse des Linearschlittens m_L und die Beschleunigung a die bestimmenden Größen für die Antriebsauslegung von Lineartrieben. Auf der Seite Bestimmung von Riementyp und Riemenbreite kann nach dem Auswahl-Diagramm Riementyp und Zahnriemenbreite aus Masse und Beschleunigung ermittelt werden.
Im Zusammenhang der Grobauslegung ist es zweckmäßig, die Zahnscheibenabmessungen (vorläufig) anzunehmen. Es sind die zulässigen Mindestzähnezahlen bzw. Mindestdurchmesser zu beachten.

Die Antriebsstation

Die erforderliche Umfangskraft F_U in der Antriebsstation ist nach Gleichung (4) zu ermitteln. Mit der vorläufigen Annahme der Zahnscheibengröße kann für die Antriebsstation das zugehörige Antriebs-Drehmoment M nach Gleichung (2) berechnet werden. Es hängt von der Art und Wahl des Antriebsmotors ab, inwieweit das berechnete Drehmoment M mit dem Drehmomentverlauf des Motors in Einklang gebracht werden kann. Die Wahl des Motors hängt auch von den gewünschten Stell- und Positionieraufgaben ab. Nach der Festlegung des Antriebsmotors ist als Berechnungsgrundlage zur weiteren Genauauslegung des Zahnriemens der tatsächliche Drehmomentverlauf des Motors heranzuziehen.

Formelsammlung

Berechnung

Berechnungsgröße

Berechnung

Berechnungsgröße

Berechnung

Berechnungsgröße

Vorgehensweise

Allgemeine Kinematik

Grobauslegung nach Masse und Beschleunigung

Die Antriebsstation

MULCO-EUROPE EWIV

Quicklinks

Rechtliches

Anmeldung

Berechnung

Berechnungsgröße

Berechnung

Berechnungsgröße

Berechnung

Berechnungsgröße

Vorgehensweise

Allgemeine Kinematik

Grobauslegung nach Masse und Beschleunigung

Die Antriebsstation